
Sacred Texts Sky Lore Index Previous Next
Buy this Book at Amazon.com

Harmonies of the World, by Johannes Kepler, tr. Charles Glenn Wallis [1939], at sacred-texts.com
First of all, my readers should know that the ancient astronomical hypotheses of Ptolemy, in the fashion in which they have been unfolded in the Theoricae of Peurbach and by the other writers of epitomes, are to be completely removed
from this discussion and cast out of [275] the mind. For they do not convey the true lay out of the bodies of the world and the polity of the movements.
Although I cannot do otherwise than to put solely Copernicus’ opinion concerning the world in the place of those hypotheses and, if that were possible, to persuade everyone of it; but because the thing is still new among the mass of the intelligentsia [apud vulgus studiosorum], and the doctrine that the Earth is one of the planets and moves among the stars around a motionless sun sounds very absurd to the ears of most of them: therefore those who are shocked by the unfamiliarity of this opinion should know that these harmonical speculations are possible even with the hypotheses of Tycho Brahe—because that author holds, in common with Copernicus, everything else which pertains to the lay out of the bodies and the tempering of the movements, and transfers solely the Copernican annual movement of the Earth to the whole system of planetary spheres and to the sun, which occupies the centre of that system, in the opinion of both authors. For after this transference of movement it is nevertheless true that in Brahe the Earth occupies at any time the same place that Copernicus gives it, if not in the very vast and measureless region of the fixed stars, at least in the system of the planetary world. And accordingly, just as he who draws a circle on paper makes the writing-foot of the compass revolve, while he who fastens the paper or tablet to a turning lathe draws the same circle on the revolving tablet with the foot of the compass or stylus motionless; so too, in the case of Copernicus the Earth, by the real movement of its body, measures out a circle revolving midway between the circle of Mars on the outside and that of Venus on the inside; but in the case of Tycho Brahe the whole planetary system (wherein among the rest the circles of Mars and Venus are found) revolves like a tablet on a lathe and applies to the motionless Earth, or to the stylus on the lathe, the midspace between the circles of Mars and Venus; and it comes about from this movement of the system that the Earth within it, although remaining motionless, marks out the same circle around the sun and midway between Mars and Venus, which in Copernicus it marks out by the real movement of its body while the system is at rest. Therefore, since harmonic speculation considers the eccentric movements of the planets, as if seen from the sun, you may easily understand that if any observer were stationed on a sun as much in motion as you please, nevertheless for him the Earth, although at rest (as a concession to Brahe), would seem to describe the annual circle midway between the planets and in an intermediate length of time. Wherefore, if there is any man of such feeble wit that he cannot grasp the movement of the earth among the stars, nevertheless he can take pleasure in the most excellent spectacle of this most divine construction, if he applies to their image in the sun whatever he hears concerning the daily movements of the Earth in its eccentric—such an image as Tycho Brahe exhibits, with the Earth at rest.
And nevertheless the followers of the true Samian philosophy have no just cause to be jealous of sharing this delightful speculation with such persons, because their joy will be in many ways more perfect, as due to the consummate perfection of speculation, if they have accepted the immobility of the sun and the movement of the earth.
Firstly [I], therefore, let my readers grasp that today it is absolutely certain among all astronomers that all the planets revolve around the sun, with the exception of the moon, which alone has the Earth as its centre: the magnitude
of the moon's sphere or orbit is not great enough for it to be delineated in this diagram in a just ratio to the rest. Therefore, to the other five planets, a sixth, the Earth, is added, which traces a sixth circle around the sun, whether by its own proper movement with the sun at rest, or motionless itself and with the whole planetary system revolving.
Secondly [II]: It is also certain that all the planets are eccentric, i.e., they change their distances from the
 Click to enlarge |
Thirdly [III]: Let the reader recall from my Mysterium Cosmographicum, which I published twenty-two years ago, that the number of the planets or circular routes around the sun was taken by the very wise Founder from the five regular solids, concerning which Euclid, so many ages ago, wrote his book which is called the Elements in that it is built up out of a series of propositions. But it has been made clear in the second book of this work that there cannot be more
regular bodies, i.e., that regular plane figures cannot fit together in a solid more than five times.
Fourthly [IV]: As regards the ratio of the planetary orbits, the ratio between two neighbouring planetary orbits is always of such a magnitude that it is easily apparent that each and every one of them approaches the single ratio of the spheres of one of the five regular solids, namely, that of the sphere circumscribing to the sphere inscribed in the figure. Nevertheless it is not wholly equal, as I once dared to promise concerning the final perfection of astronomy. For, after completing the demonstration of the intervals from Brahe's observations, I discovered the following: if the angles of the cube [277] are applied to the inmost circle of Saturn, the centres of the planes are approximately tangent to the middle circle of Jupiter; and if the angles of the tetrahedron are placed against the inmost circle of Jupiter, the centres of the planes of the tetrahedron are approximately tangent to the outmost circle of Mars; thus if the angles of the octahedron are placed against any circle of Venus (for the total interval between the three has been very much reduced), the centres of the planes of the octahedron penetrate and descend deeply within the outmost circle of Mercury, but nonetheless do not reach as far as the middle circle of Mercury; and finally, closest of all to the ratios of the dodecahedral and icosahedral spheres—which ratios are equal to one another—are the ratios or intervals between the circles of Mars and the Earth, and the Earth and Venus; and those intervals are similarly equal, if we compute from the inmost circle of Mars to the middle circle of the Earth, but from the middle circle of the Earth to the middle circle of Venus. For the middle distance of the Earth is a mean proportional between the least distance of Mars and the middle distance of Venus. However, these two ratios between the planetary circles are still greater than the ratios of those two pairs of spheres in the figures, in such fashion that the centres of the dodecahedral planes are not tangent to the outmost circle of the Earth, and the centres of the icosahedral planes are not tangent to the outmost circle of Venus; nor, however, can this gap be filled by the semidiameter of the lunar sphere, by adding it, on the upper side, to the greatest distance of the Earth and subtracting it, on the lower, from the least distance of the same. But I find a certain other ratio of figures—namely, if I take the augmented dodecahedron, to which I have given the name of echinus, (as being fashioned from twelve quinquangular stars and thereby very close to the five regular solids), if I take it, I say, and place its twelve points in the inmost circle of Mars, then the sides of the pentagons, which are the bases of the single rays or points, touch the middle circle of Venus. In short: the cube and the octahedron, which are consorts, do not penetrate their planetary spheres at all; the dodecahedron and the icosahedron, which are consorts, do not wholly reach to theirs, the tetrahedron exactly touches both: in the first case there is falling short; in the second, excess; and in the third, equality, with respect to the planetary intervals.
Wherefore it is clear that the very ratios of the planetary intervals from the sun have not been taken from the regular solids alone. For the Creator, who is the very source of geometry and, as Plato wrote, "practices eternal geometry," does not stray from his own archetype. And indeed that very thing could be inferred from the fact that all the planets change their intervals throughout fixed periods of time, in such fashion that each has two marked intervals from the sun, a greatest and a least; and a fourfold comparison of the intervals from the
sun is possible between two planets: the comparison can be made between either the greatest, or the least, or the contrary intervals most remote from one another, or the contrary intervals nearest together. In this way the comparisons made two by two between neighbouring planets are twenty in number, although on the contrary there are only five regular solids. But it is consonant that if the Creator had any concern for the ratio of the spheres in general, He would also have had concern for the ratio which exists between the varying intervals of the single planets specifically and that the concern is the same in both cases and the one is bound up with the other. If we ponder that, we will comprehend that for setting up the diameters and eccentricities conjointly, there is need of more principles, outside of the five regular solids.
Fifthly [V]: To arrive at the movements between which the consonances have been set up, once more I impress upon the reader that in the Commentaries on Mars I have demonstrated from the sure observations of Brahe that daily arcs, which are equal in one and the same eccentric circle, are not traversed with equal speed; but that these differing delays in equal parts of the eccentric observe the ratio of their distances from the sun, the source of movement; and conversely, that if equal times are assumed, namely, one natural day in both cases, the corresponding true diurnal arcs [278] of one eccentric orbit have to one another the ratio which is the inverse of the ratio of the two distances from the sun. Moreover, I demonstrated at the same time that the planetary orbit is elliptical and the sun, the source of movement, is at one of the foci of this ellipse; and so, when the planet has completed a quarter of its total circuit from its aphelion, then it is exactly at its mean distance from the sun, midway between its greatest distance at the aphelion and its least at the perihelion. But from these two axioms it results that the diurnal mean movement of the planet in its eccentric is the same as the true diurnal arc of its eccentric at those moments wherein the planet is at the end of the quadrant of the eccentric measured from the aphelion, although that true quadrant appears still smaller than the just quadrant. Furthermore, it follows that the sum of any two true diurnal eccentric arcs, one of which is at the same distance from the aphelion that the other is from the perihelion, is equal to the sum of the two mean diurnal arcs. And as a consequence, since the ratio of circles is the same as that of the diameters, the ratio of one mean diurnal arc to the sum of all the mean and equal arcs in the total circuit is the same as the ratio of the mean diurnal arc to the sum of all the true eccentric arcs, which are the same in number but unequal to one another. And those things should first be known concerning the true diurnal arcs of the eccentric and the true movements, so that by means of them we may understand the movements which would be apparent if we were to suppose an eye at the sun.
Sixthly [VI]: But as regards the arcs which are apparent, as it were, from the sun, it is known even from the ancient astronomy that, among true movements which are equal to one another, that movement which is farther distant from the centre of the world (as being at the aphelion) will appear smaller to a beholder at that centre, but the movement which is nearer (as being at the perihelion) will similarly appear greater. Therefore, since moreover the true diurnal arcs at the near distance are still greater, on account of the faster movement, and still smaller at the distant aphelion, on account of the slowness of the movement, I demonstrated in the Commentaries on Mars that the ratio of the apparent diurnal arcs of one eccentric circle is fairly exactly the inverse ratio of the squares of their distances from the sun. For example, if the planet one day when it is at
a distance from the sun of 10 parts, in any measure whatsoever, but on the opposite day, when it is at the perihelion, of 9 similar parts: it is certain that from the sun its apparent progress at the aphelion will be to its apparent progress at the perihelion, as 81 : 100.
But that is true with these provisos: First, that the eccentric arcs should not be great, lest they partake of distinct distances which are very different—i.e., lest the distances of their termini from the apsides cause a perceptible variation; second, that the eccentricity should not be very great, for the greater its eccentricity (viz., the greater the arc becomes) the more the angle of its apparent movement increases beyond the measure of its approach to the sun, by Theorem 8 of Euclid's Optics; none the less in small arcs even a great distance is of no moment, as I have remarked in my Optics, Chapter 11. But there is another reason why I make that admonition. For the eccentric arcs around the mean anomalies are viewed obliquely from the centre of the sun. This obliquity subtracts from the magnitude of the apparent movement, since conversely the arcs around the apsides are presented directly to an eye stationed as it were at the sun. Therefore, when the eccentricity is very great, then the eccentricity takes away perceptibly from the ratio of the movements; if without any diminution we apply the mean diurnal movement to the mean distance, as if at the mean distance, it would appear to have the same magnitude which it does have—as will be apparent below in the case of Mercury. All these things are treated at greater length in Book V of the Epitome of Copernican Astronomy; but they have been mentioned here too because they have to do with the very terms of the celestial consonances, considered in themselves singly and separately.
Seventhly [VII]: If by chance anyone runs into those diurnal movements which are apparent [279] to those gazing not as it were from the sun but from the Earth, with which movements Book VI of the Epitome of Copernican Astronomy deals, he should know that their rationale is plainly not considered in this business. Nor should it be, since the Earth is not the source of the planetary movements, nor can it be, since with respect to deception of sight they degenerate not only into mere quiet or apparent stations but even into retrogradation, in which way a whole infinity of ratios is assigned to all the planets, simultaneously and equally. Therefore, in order that we may hold for certain what sort of ratios of their own are constituted by the single real eccentric orbits (although these too are still apparent, as it were to one looking from the sun, the source of movement), first we must remove from those movements of their own this image of the adventitious annual movement common to all five, whether it arises from the movement of the Earth itself, according to Copernicus, or from the annual movement of the total system, according to Tycho Brahe, and the winnowed movements proper to each planet are to be presented to sight.
Eighthly [viii]: So far we have dealt with the different delays or arcs of one and the same planet. Now we must also deal with the comparison of the movements of two planets. Here take note of the definitions of the terms which will be necessary for us. We give the name of nearest apsides of two planets to the perihelion of the upper and the aphelion of the lower, notwithstanding that they tend not towards the same region of the world but towards distinct and perhaps contrary regions. By extreme movements understand the slowest and the fastest of the whole planetary circuit; by converging or converse extreme movements, those which are at the nearest apsides of two planets—namely, at the
perihelion of the upper planet and the aphelion of the lower; by diverging or diverse, those at the opposite apsides—namely, the aphelion of the upper and the perihelion of the lower. Therefore again, a certain part of my Mysterium Cosmographicum, which was suspended twenty-two years ago, because it was not yet clear, is to be completed and herein inserted. For after finding the true intervals of the spheres by the observations of Tycho Brahe and continuous labour and much time, at last, at last the right ratio of the periodic times to the spheres
and, if you want the exact time, was conceived mentally on the 8th of March in this year One Thousand Six Hundred and Eighteen but unfelicitously submitted to calculation and rejected as false, finally, summoned back on the 15th of May, with a fresh assault undertaken, outfought the darkness of my mind by the great proof afforded by my labor of seventeen years on Brahe's observations and meditation upon it uniting in one concord, in such fashion that I first believed I was dreaming and was presupposing the object of my search among the principles. But it is absolutely certain and exact that the ratio which exists between the periodic times of any two planets is precisely the ratio of the 3/2th power of the mean distances, i.e., of the spheres themselves; provided, however, that the arithmetic mean between both diameters of the elliptic orbit be slightly less than the longer diameter. And so if any one take the period, say, of the Earth, which is one year, and the period of Saturn, which is thirty years, and extract the cube roots of this ratio and then square the ensuing ratio by squaring the cube roots, he will have as his numerical products the most just ratio of the distances of the Earth and Saturn from the sun. 1 For the cube root of 1 is 1, and the square of it is 1; and the cube root of 30 is greater than 3, and therefore the square of it is greater than 9. And Saturn, at its mean distance from the sun, is slightly higher [280] than nine times the mean distance of the Earth from the sun. Further on, in Chapter 9, the use of this theorem will be necessary for the demonstration of the eccentricities.
Ninthly [IX]: If now you wish to measure with the same yardstick, so to speak, the true daily journeys of each planet through the ether, two ratios are to be compounded—the ratio of the true (not the apparent) diurnal arcs of the eccentric, and the ratio of the mean intervals of each planet from the sun (because that is the same as the ratio of the amplitude of the spheres), i.e., the true diurnal arc of each planet is to be multiplied by the semidiameter of its sphere: the products will be numbers fitted for investigating whether or not those journeys are in harmonic ratios.
Tenthly [X]: In order that you may truly know how great any one of these diurnal journeys appears to be to an eye stationed as it were at the sun, although this same thing can be got immediately from the astronomy, nevertheless it will also be manifest if you multiply the ratio of the journeys by the inverse ratio not of the mean, but of the true intervals which exist at any position on
the eccentrics: multiply the journey of the upper by the interval of the lower planet from the sun, and conversely multiply the journey of the lower by the interval of the upper from the sun.
Eleventhly [XI]: And in the same way, if the apparent movements are given, at the aphelion of the one and at the perihelion of the other, or conversely or alternately, the ratios of the distances of the aphelion of the one to the perihelion of the other may be elicited. But where the mean movements must be known first, viz., the inverse ratio of the periodic times, wherefrom the ratio of the spheres is elicited by Article VIII above: then if the mean proportional between the apparent movement of either one of its mean movement be taken, this mean proportional is to the semidiameter of its sphere (which is already known) as the mean movement is to the distance or interval sought. Let the periodic times of two planets be 27 and 8. Therefore the ratio of the mean diurnal movement of the one to the other is 8 : 27. Therefore the semidiameters of their spheres will be as 9 to 4. For the cube root of 27 is 3, that of 8 is 2, and the squares of these roots, 3 and 2, are 9 and 4. Now let the apparent aphelial movement of the one be 2 and the perihelial movement of the other 33⅓. The mean proportionals between the mean movements 8 and 27 and these apparent ones will be 4 and 30. Therefore if the mean proportional 4 gives the mean distance of 9 to the planet, then the mean movement of 8 gives an aphelial distance 18, which corresponds to the apparent movement 2; and if the other mean proportional 30 gives the other planet a mean distance of 4, then its mean movement of 27 will give it a perihelial interval of 3 3/5. I say, therefore, that the aphelial distance of the former is to the perihelial distance of the latter as 18 to 3 3/5. Hence it is clear that if the consonances between the extreme movements of two planets are found and the periodic times are established for both, the extreme and the mean distances are necessarily given, wherefore also the eccentricities.
Twelfthly [XII]: It is also possible, from the different extreme movements of one and the same planet, to find the mean movement. The mean movement is not exactly the arithmetic mean between the extreme movements, nor exactly the geometric mean, but it is as much less than the geometric mean as the geometric mean is less than the [arithmetic] mean between both means. Let the two extreme movements be 8 and 10: the mean movement will be less than 9, and also less than the square root of 80 by half the difference between 9 and the square root of 80. In this way, if the aphelial movement is 20 and the perihelial 24, the mean movement will be less than 22, even less than the square root of 480 by half the difference between that root and 22. There is use for this theorem in what follows.
[281] Thirteenthly [XIII]: From the foregoing the following proposition is demonstrated, which is going to be very necessary for us: Just as the ratio of the mean movements of two planets is the inverse ratio of the 3/2th powers of the spheres, so the ratio of two apparent converging extreme movements always falls short of the ratio of the 3/2th powers of the intervals corresponding to those extreme movements; and in what ratio the product of the two ratios of the corresponding intervals to the two mean intervals or to the semidiameters of the two spheres falls short of the ratio of the square roots of the spheres, in that ratio does the ratio of the two extreme converging movements exceed the ratio of the corresponding intervals; but if that compound ratio were to exceed the
ratio of the square roots of the spheres, then the ratio of the converging movements would be less than the ratio of their intervals. 1
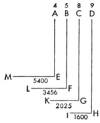
Let the ratio of the spheres be DH : AE; let the ratio of the mean movements be HI : EM, the 3/2th power of the inverse of the former.
 Click to enlarge |
I say that
For
and
Hence
But
by a fixed ratio of defect, as was assumed. Therefore too
by a ratio of defect which is the square of the former. But by number VIII
Therefore let the ratio which is smaller by the total square of the ratio of defect be divided into the ratio of the 3/2th powers; that is,
by the excess squared. But
Therefore
by the excess squared. But
And
by the simple defect. Therefore
by the simple excess. But
but by the excess squared. But the excess squared is greater than the simple excess. Therefore the ratio of the movements GK to FL is greater than the ratio of the corresponding intervals BF to CG.
In fully the same way, it is demonstrated even contrariwise that if the planets approach one another in G and F beyond the mean distances in H and E, in such fashion that the ratio of the mean distances DH : AE becomes less than DH½ : AE½, then the ratio of the movements GK : FL becomes less than the ratio of the corresponding intervals BF: CG. For you need to do nothing more than to change the words greater to less, > to <, excess to defect, and conversely.
In suitable numbers, because the square root of 4/9 is 2/3; and 5/8 is even greater than 2/3 by the ratio of excess 15/16; and the square of the ratio 8 : 9 [282] is the ratio 1600 : 2025, i.e., 64 : 81; and the square of the ratio 4 : 5 is the ratio 3456 : 5400, i.e., 16 : 25; and finally the 3/2th power of the ratio 4 : 9 is the ratio 1600 : 5400, i.e., 8 : 27: therefore too the ratio 2025 : 3456, i.e., 75 : 128, is even greater than 5 : 8, i.e., 75 : 120, by the same ratio of excess (i.e., 120 : 128), 15 : 16; whence 2025 : 3456, the ratio of the converging movements, exceeds 5 : 8, the inverse ratio of the corresponding intervals, by as much as 5 : 8 exceeds 2 : 3, the square root of the ratio of the spheres. Or, what amounts to the same thing, the ratio of the two converging intervals is a mean between the ratio of the square roots of the spheres and the inverse ratio of the corresponding movements.
Moreover, from this you may understand that the ratio of the diverging movements is much greater than the ratio of the 3/2th powers of the spheres, since the ratio of the 3/2th powers is compounded with the squares of the ratio of the aphelial interval to the mean interval, and that of the mean to the perihelial.
1020:1 For in the Commentaries on Mars, chapter 48, page 232, I have proved that this Arithmetic mean is either the diameter of the circle which is equal in length to the elliptic orbit, or else is very slightly less.
1022:1 Kepler always measures the magnitude of a ratio from the greater term to the smaller, rather than from the antecedent to the consequent, as we do today. For example, as Kepler speaks, 2 : 3 is the same as 3 : 2, and 3 : 4 is greater than 7 : 8.—C. G. Wallis.