
Sacred Texts Miscellaneous Index Previous Next
Buy this Book at Amazon.com

Mazes and Labyriths, by W. H. Matthews, [1922], at sacred-texts.com
THERE is no limit to the number of patterns which, without any metaphorical extension of terms, we may legitimately describe as coming within the scope of the words "maze" and "labyrinth." In common speech we use either word to describe any artificial design or natural pattern presenting a convoluted appearance, or any path or channel of an intricate nature, but when we come to consider the matter more carefully we feel the need for some definition. As we have seen, the dictionaries do not help us much in this respect. Let us, therefore, decide what limitations we feel compelled to observe in our use of the terms from the point of view of designers or unravellers of mazes and labyrinths.
In the first place we must limit ourselves to works of artifice, i.e., we must exclude the "labyrinths" of nature, such as forests, caverns, and so forth, and agree that any application of our terms to such objects is to be regarded as strictly metaphorical.
Secondly, we must require, as a practical corollary to our first condition, that there shall be an element of purposefulness in the design. The purpose may be the portrayal of the imagined course of the sun through the heavens, the symbolisation of the folds of sin or of the Christian's toilsome journey through life, the construction of a puzzle, or the mere pleasure to be derived from packing
the maximum of path into the minimum of space, but there must be an object of some sort. The aimless scribblings of an infant, like the trail of an ink-dipped fly, may in this connection be considered as the fortuitous meanderings of nature rather than the conscious design of man. By imposing this condition we exclude the Indian pictograph shown in Fig. 132, which, in the absence of any indication as to its significance, can only by a loose extension of the term be called a labyrinth.
(Our use of the words "aim," "design," and "purpose" will be quite clear to everybody but the sciolist dabbling in metaphysics.)
Thirdly, there must be a certain degree of complexity in the design, a degree which it is manifestly impossible to define as it must be considered in conjunction with other characteristics in any particular case. In the case of a unicursal labyrinth, i.e., one in which there is only one path, the complexity lies in the multiplicity of turnings and the extent of the departure from pure geometrical figures such as the meander, the zigzag, and the spiral; in the case of a puzzle-figure it lies partly in this but partly also in the number and disposition of branch-paths. It naturally follows that in a unicursal design there cannot be absolute symmetry, although, with a little ingenuity, a very pleasing appearance of symmetry may be obtained.
Fourthly, there must be communication between the component parts of the design; in other words, the path must be continuous. This does not preclude the occurrence in the design of closed "islands," but only makes it clear that such inclusions do not form part of the labyrinth proper.
Fifthly, there must be communication between the interior and the exterior. We might not altogether with-hold the application of the term "labyrinth" or "maze" in the case of a closed design, but we should have to qualify it, e.g., by prefixing the word "closed." In the
case of the beautiful and intricate mosaic pavement found in the Casa del Labirinto at Pompeii mentioned on page 46, for example, although we know that the pattern was intended to convey an allusion to the Cretan labyrinth, we cannot look upon it as a true labyrinth design; not only is there no communication with the exterior, but by its repetition of purely geometrical design it fails to satisfy our third condition.
If the reader chooses to formulate for himself a working definition based on the above remarks he is at liberty to do so, but he may take for granted that nobody else will accept it. However, he will have gained, at any rate, a clearer conception of the matter than he would perhaps have gathered from any dictionary.
We have seen that mazes and labyrinths may be roughly divided into two types as regards the principle of their design, namely, into unicursal and multicursal types, or, as some say, into "non-puzzle" and "puzzle" types respectively. The word "unicursal" has hitherto been chiefly used by mathematicians to describe a class of problems dealing with the investigation of the shortest route between two given points or of the method of tracing a route between two points in a given figure without covering any part of the ground more or less than once (e.g., the well-known "bridge" problems), but there is no reason why we should not apply the adjective "unicursal" (= "single course" or "once run") to denote those figures which consist of a single unbranched path, using the term "multicursal" as its complement, or antonym. We must not draw too hard a line between these two types; for instance, we could not reasonably insist that the turf maze at Wing (Fig. 60) is multicursal simply on account of the dichotomy of its path to form the central loop. Where the loop is itself relatively large and complex, as in the Poitiers example (Fig. 55), there are better grounds for doing so, but it is plain that in such cases the point is one to be decided by common-sense.
Let us consider a little further the various forms of labyrinth design and make some sort of a classification.
In the first place we may observe that a labyrinth (using this word, for convenience, as embracing "maze") may be arranged in one plane, as we commonly see it on a sheet of paper, or it may be disposed in two or more intercommunicating planes, like the Egyptian labyrinth or a block of flats. We may thus classify all labyrinths, for a start, as either two-dimensional or three-dimensional. As the vast majority belong to the first class and as, moreover, every subdivision of the first class may be applied equally to the second, we need say no more concerning the latter except to remark that the complexity of a garden maze may be greatly increased, if desired, by introducing tunnels or bridges, thus converting it into a three-dimensional maze.
Another general grouping of labyrinths would be into "compact" and "diffuse" types, the former having, in a typical case, the whole of its area occupied by the convolutions of its path and its bounding walls, the latter having spaces between the bounding walls of the various sections of the path, such spaces having no communication with the path itself. Amongst unicursal labyrinths the Alkborough specimen (Fig. 59) exemplifies the compact type and the Pimperne maze (Fig. 63) the diffuse type.
The Hampton Court maze (Fig. 111) may serve as the type of a compact and the Versailles example (Fig. 88) that of a diffuse multicursal labyrinth.
With regard to the nature of the path itself, we may distinguish broadly between labyrinths with curved and those with straight paths, allowing for an intermediate "mixed" group in which part of the path is curved and part straight. Examples of each kind will be found amongst the figures given.
Multicursal mazes, again, may be subdivided according to the manner of branching of the path, e.g.,
according to whether the branches are simple or sub-divided (the occurrence of more than one branch at any point may be considered as the case of a subdivided branch), whether the branches do or do not rejoin the main path, forming "loops," and whether—a rather important point as regards the solution of the maze—the "goal" is or is not situated within a loop.
Finally we may create separate classes for those mazes in which there are two or more equivalent routes between the entrance and the goal, those which have two or more entrances, and those in which there is no distinct goal (e.g., the Versailles maze) or in which there are two or more equivalent goals.
We can represent the branch system of any labyrinth whatever in a very simple manner by means of a straight-line diagram, wherein the paths of the labyrinth are represented by lines, to scale if need be, branches being shown to the left or right respectively of the main straight line representing the shortest path from the entrance to the goal. It will be seen that no account is taken of the actual orientation or of changes of direction of any part of the path.
A unicursal labyrinth will thus be represented by a single straight line. Figs. 136 and 137 represent, roughly to scale, the Hampton Court and Hatfield mazes respectively and should be compared with those shown in Figs. 111 and 87. Triangles and discs may be used, as shown, to indicate entrances and goals respectively.
Such diagrams as these are just as useful as the actual plans of the mazes for the purpose of serving as a clue for the visitor; in fact, they are really more easily followed.
Amongst the many speculations that have from time to time been made regarding the origin and significance of the design on the Knossian coins, the suggestion was made by a contributor to Knowledge about thirty years ago—somewhat similar theories having been expounded by a German writer a decade earlier—that this figure
was a simplified diagram comparable with the diagrams described above. According to this conception the figure was intended as a clue to the actual labyrinth, the designs on the coins being perhaps copied from those on "souvenir" tokens issued by the priests or curators of the edifice, and indicated the right path to be taken, all other paths being omitted. By splitting the circular dividing walls so as to form a passage of the same width as the path shown in the figure, a maze of much more intricate appearance was arrived at, which, it was thought, might
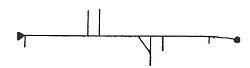
FIG. 136.—Straight-line Diagram, Hampton Court Maze.
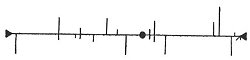
FIG. 137.—Straight-line Diagram, Hatfield Maze.
bear some resemblance to the form of the original labyrinth.
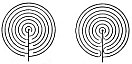
On the other hand, Dr. E. Krause, in a book of about the same date, showed how the Knossian design and certain other unicursal figures might be derived from a series of concentric circles, with interruptions along a radial line like the figures in the northern rock engravings described in Chapter XVII, by means of one or two simple methods of cross-connection (Figs. 138 and 139).
Such speculations give food for thought, but we must remember that so far they are speculations and not statements of fact.
The use of the straight-line diagrams suggested above may be found helpful not only as a means of facilitating the study of an existing labyrinth, but also to some extent in designing a new one. It is not necessary to describe here in detail how to design a maze:
and, like most tasks requiring simply common-sense, patience, and practice, it is much more trouble to explain than to perform. As regards the design of hedge mazes,
Click to enlarge
FIGS. 138 and 139.—Derivation of Labyrinth Types from Rock-engraving Figures. (After Krause.)
the fact that the circumstances are hardly ever alike in any two actual cases gives plenty of scope for individuality and ingenuity. The space allowed may be strictly limited, or it may be of an awkward shape. The materials avail-able for the walls may vary widely in character according to the space they require for their proper growth and maintenance, and thus affect the amount of path-area.
There are one or two points which are of general application and should be borne in mind. For instance, if the object of the designer is to provide a maze which shall offer a fair amount of puzzledom without imposing undue fatigue on the visitor, he must take care that the nearest route from the centre to the exterior be neither too long
nor too short. If the space to be covered by the maze is large the tendency to over-elaboration of the design must be avoided.
Another feature which is likely to spoil an otherwise good design is the inclusion of long stretches of path without bend or branching; these are tedious and annoying, especially when they have to be retraced by reason of their leading into a cul-de-sac.
In a large maze it is well to relieve monotony by means of occasional variations in the mode of treatment of the hedge, the introduction of arbours, statues, etc.; but these should not be of such a character as to defeat one of the main objects of the design by providing easy clues.
If the maze is intended to be seen at all from above, some attempt should be made to introduce a symmetrical and artistic element into its design. Usually some vantage-point is available from which an attendant or expert can observe and direct over-bewildered visitors, but if this point be accessible to the visitors themselves the hedges should be provided with pinnacles or balks, here and there, to prevent the observer from solving the puzzle by unfair means. This is the case with, for instance, the Saffron Walden maze; at Hampton Court, where there are no balks, only the attendant is permitted to mount the rostrum.
The "solution" of mazes means the discovery of a route to their "goal." (This word is preferable to "centre," as the object of quest is not necessarily at the geometrical centre of the maze, but may be considerably removed from it.)
It would be going too far to say the shortest route, as this would be discoverable only from the plan or by prolonged experience, but the goal in any maze will on the average be reached more certainly and quickly by observing a little method than by fortuitous wandering.
The subject of the solution of mazes has been examined by various mathematicians, in their lighter moods,
but we need not burden ourselves with more than a few simple considerations.
In most cases it is not practicable to adopt a system of marking the various paths as we reach them, but if this be permitted we can so arrange our marks that we need never traverse any portion of the path more than twice—i.e., once in each direction—so that in any finite maze we must eventually arrive at the goal, though not necessarily by the shortest route.
Using the word node to signify a point of branching, and the terms odd and even to describe respectively those nodes at which odd or even numbers of paths are to be found, we see that there must be at least three paths meeting at a point to form a node, for two paths meeting at a point constitute only a change of direction of the path without formation of branches, whilst the arrival of one path only at a point also precludes the idea of "branching" at that point, and can only occur at the end of a blind alley, at the entrance of the maze, or at the goal. We find it convenient, however, to regard the latter arrangement as an odd node of the lowest order, the lowest possible order of even nodes being, of course, that at the meeting of four paths.
It will be clear that if the entrance and the goal are the only odd nodes the maze will either be unicursal, in the sense in which we have been using the term, or any branches must form loops on the main route; in either case it will be possible to traverse the maze unicursally, i.e., to thread every portion of the path without going over any part twice.
Supposing that we are able to make what marks we like, without danger of their removal in our absence, we can adopt the following plan:
On arriving at a node which, by the absence of marks, you know you have not already visited, mark the path by which you have just arrived by three marks; if you see by marks on other paths that you have already been to
that node, mark the arrival path with one mark only. If now there are no unmarked paths at this node, it means that you have explored this particular branch-system and must retrace your steps by the path by which you have arrived. If, however, there are one or more unmarked paths leading from the node, select one of them, and, as you enter it, mark it with two marks.
We can now make certain of visiting every part of the maze if we make it a rule that, on arrival at a node, we shall never take a path with three marks unless there are no paths unmarked or with one mark only. When we enter a one-mark path, we of course add the two marks which we always make on leaving a node, and thus it becomes a three-mark path at that node.
When it is impracticable to place marks, or even to use, like Theseus, a clue of thread, it is still possible in the majority of cases to make certain of finding the goal by the simple expedient of placing one hand on the hedge on entering the maze, and consistently following the hedge around, keeping contact all the time with the same hand. Blind turnings present no difficulty, as they will only be traversed first in one direction and then in the other. The traveller being guided by his contact with the hedge alone is relieved of all necessity for making a choice of paths when arriving at the nodes.
The only case in which this method breaks down is that in which the goal is situated anywhere within a loop. Where this occurs the explorer adopting the method described will discover the fact by finding himself eventually back at the starting-point without having visited the goal. He must then adopt different tactics, but unless it is practicable to use a clue or a system of marks like that detailed above there is no rule that will help him. One may, of course, thread the maze by remembering a formula of some sort applicable to that particular maze, e.g., in the case of Hampton Court, "Left, right, right, left, left, left, left," but this is equivalent to having a plan
of the maze. Such mnemonics, unless perfectly retained, are apt to prove more of a nuisance than a help.
Can anybody who has once yielded to the exuberant mirth of "Three Men in a Boat" forget the predicament of the over-confident Harris when he volunteered to conduct a party, strangers as well, through the Hampton Court maze? "We'll just go in here," he said, "so that you can say you've been, but it's very simple. It's absurd to call it a maze. You keep on taking the first turning to the right. We'll just walk round for ten minutes and then go and get some lunch." Poor Harris!